[패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 11회차 미션 Programming/Python2020. 11. 12. 11:13
[파이썬을 활용한 데이터 전처리 Level UP- 11 회차 미션 시작]
* 복습
- EDA 과정을 통해서 우리가 모르는 데이터간의 상관관계에 대한 이해나 다각도로 접근할 수 있는 시각에 대해서 다시 한번 생각해 볼 수 있었다.
[02. Part 2) 탐색적 데이터 분석 Chapter 09. 변수가 어떻게 생겼나 - 기초 통계 분석 - 01. 기초 통계 분석을 해야 하는 이유]

* 확률 변수의 정의
- 변수 (variable) : 특정 조건에 따라 변하는 값
// 조건이 없을 수도 있지만 어떤 조건에 따라서 변하는 값이다.
- 확률 변수 (random variable): 특정 값(범위)을 확률에 따라 취하는 변수
. 예시 : 주사위를 던졌을 때 나오는 결과를 나타내는 변수 X
// 주사위나 동전을 던졌을 때

- 상태 공간의 크기가 무한한 변수를 연속 확률 변수, 유한한 변수를 이산 확률 변수라고 한다.
// float 나 string 이라고 무한, 유한 이라고 보면 안되고, 자료가 엄청 많다면 연속 확률 변수, 자료가 그렇게 많지 않다면 이산 확률 변수이다.
- 우리가 관측하는 데이터에 있는 변수는 특별한 경우를 제외하곤 모두 확률 변수이다.
* 확률 분포의 정의
- 확률 분포(probability distribution)는 확률 변수가 특정한 값을 취할 확률을 나타내는 함수를 의미한다.
// 주사위의 확률 분포는 상수 1/6이라고 보면 된다. uniform
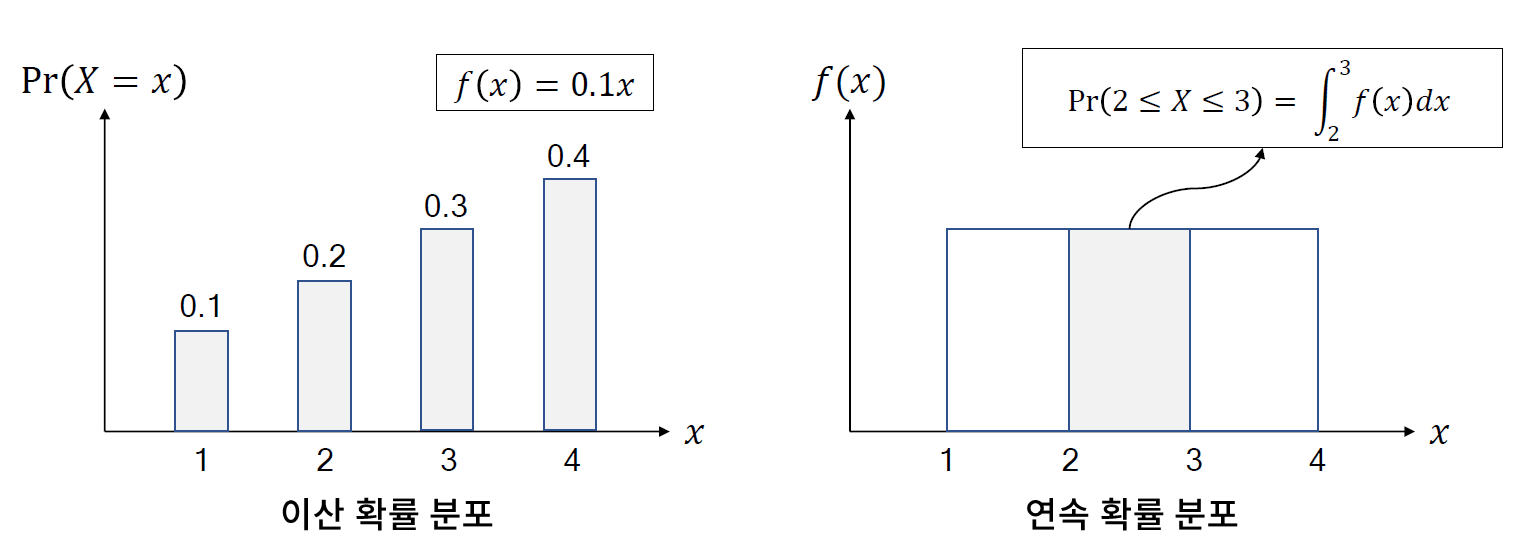
// 이산확률분포 -> 확률질량 함수, 연속확률 분포 -> 확률 밀도 함수
* 확률 분포의 확인 방법
// 특별한 경우를 제외하고는 확률에 대해서 절대 알 수가 없다. (동전 던지기, 주사위 던지기 등)
- 한 변수가 따르는 확률 분포를 확인했을 때의 효과
. (1) 현재 수집한 데이터가 어떻게 생겼는지를 이해할 수 있다.
. (2) 새로 데이터가 들어오면 어떻게 들어올 것인지 예상할 수 있다.
- 그러나 가지고 있는 데이터는 샘플 데이터이므로 절대로 정확히 한 변수가 따르는 확률 분포를 알 수 없다.
- 그래프를 이용하여 확인하거나 적합성 검정을 사용하여 확률 분포를 확인해야 하는데, 이 작업은 굉장히 많은 노력이 필요하다.
* 통계량의 필요성 : 간단하게 확률 분포의 확인
- 통계량은 확률 분포의 특성을 나타내는 지표를 의미한다.
// 어떤 변수의 특성을 나타낸다고 봐도 된다.
- 통계량을 계산하는 기초 통계 분석 (기술 통계 분석)을 바탕으로 확률 분포를 간단하게 확인 가능하다. (단, 반드시 각 통계량이 나타내는 의미를 이해해야 한다.)
- 특히, 변수가 많은 경우에 휠씬 효율적으로 사용 가능하다.
// 수학적의미가 당연히 중요하지만, 그 의미까지 일일이 파악하지 않아도 된다. 거기에 대한 이해만 하고 따라가면 된다.
* 통계량의 종류
- 통계량은 크게 대표 통계량, 산포 통계량, 분포 통계량으로 구분할 수 있다.

[02. Part 2) 탐색적 데이터 분석 Chapter 09. 변수가 어떻게 생겼나 - 기초 통계 분석 - 02. 대표 통계량]

* 평균
- 산술 평균 : 가장 널리 사용되는 평균으로 연속형 변수에 대해 사용

-> 이진 변수에 대한 산술 평균은 1의 비율과 같다.
-> 다른 관측치에 비해 매우 크거나 작은 값에 크게 영향을 받을 수 있다.
// 이상치에 매우 민감하다고 할 수 있다.
- 조화 평균 : 비율 및 변화율 등에 대한 평균을 계산할 때 사용 (데이터의 역수의 산술 평균의 역수)

// 조화 평균은 머신러닝에서 재현율과 정밀도 등을 계산할 때 쓴다.
- 절사 평균 : 데이터에서 알파 ~ 1 - 알파의 범위에 속하는 데이터에 대해서만 평균을 낸것이다.
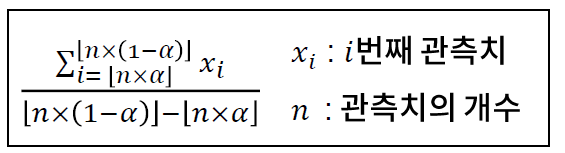
-> 매우 크거나 작은 값에 의한 영향을 줄이기 위해 고안되었다.
// 예를 들어 데이터의 순위를 매겨서 어느 특정 구간에서의 평균을 구한다.. 그래서 알파를 어떻게 설정할 것인가에 대해서 중요하게 생각해야 한다.
* 파이썬을 이용한 평균 계산

// mean method 는 scipy 에서 가져온 함수라고 생각하면 된다.
// scipy.stats 통계분서에서 많이 쓰이는 함수이다.
// numpy.mean documenation
numpy.org/doc/stable/reference/generated/numpy.mean.html
numpy.mean(a, axis=None, dtype=None, out=None, keepdims=<no value>)Compute the arithmetic mean along the specified axis.
Returns the average of the array elements. The average is taken over the flattened array by default, otherwise over the specified axis. float64 intermediate and return values are used for integer inputs.
Parameters
a array_like
Array containing numbers whose mean is desired. If a is not an array, a conversion is attempted.
axis None or int or tuple of ints, optional
Axis or axes along which the means are computed. The default is to compute the mean of the flattened array.
New in version 1.7.0.
If this is a tuple of ints, a mean is performed over multiple axes, instead of a single axis or all the axes as before.
dtype data-type, optional
Type to use in computing the mean. For integer inputs, the default is float64; for floating point inputs, it is the same as the input dtype.
out ndarray, optional
Alternate output array in which to place the result. The default is None; if provided, it must have the same shape as the expected output, but the type will be cast if necessary. See ufuncs-output-type for more details.
keepdims bool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.
If the default value is passed, then keepdims will not be passed through to the mean method of sub-classes of ndarray, however any non-default value will be. If the sub-class’ method does not implement keepdims any exceptions will be raised.
Returns
m ndarray, see dtype parameter above
If out=None, returns a new array containing the mean values, otherwise a reference to the output array is returned.
// numpy.ndarray.mean documenation
numpy.org/doc/stable/reference/generated/numpy.ndarray.mean.html
ndarray.mean(axis=None, dtype=None, out=None, keepdims=False)Returns the average of the array elements along given axis.
Refer to numpy.mean for full documentation.
// pandas.Series.mean documentation
pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.mean.html
Series.mean(axis=None, skipna=None, level=None, numeric_only=None, **kwargs)Return the mean of the values for the requested axis.
Parameters
axis {index (0)}
Axis for the function to be applied on.
skipna bool, default True
Exclude NA/null values when computing the result.
level int or level name, default None
If the axis is a MultiIndex (hierarchical), count along a particular level, collapsing into a scalar.
numeric_only bool, default None
Include only float, int, boolean columns. If None, will attempt to use everything, then use only numeric data. Not implemented for Series.
**kwargs
Additional keyword arguments to be passed to the function.
Returns
scalar or Series (if level specified)
// scipy.stats.hmean documentation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.hmean.html
scipy.stats.hmean(a, axis=0, dtype=None)Calculate the harmonic mean along the specified axis.
That is: n / (1/x1 + 1/x2 + … + 1/xn)
Parameters
a array_like
Input array, masked array or object that can be converted to an array.
axis int or None, optional
Axis along which the harmonic mean is computed. Default is 0. If None, compute over the whole array a.
dtype dtype, optional
Type of the returned array and of the accumulator in which the elements are summed. If dtype is not specified, it defaults to the dtype of a, unless a has an integer dtype with a precision less than that of the default platform integer. In that case, the default platform integer is used.
Returns
hmean ndarray
See dtype parameter above.
// scipy.stats.trim_mean documenation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.trim_mean.html
scipy.stats.trim_mean(a, proportiontocut, axis=0)Return mean of array after trimming distribution from both tails.
If proportiontocut = 0.1, slices off ‘leftmost’ and ‘rightmost’ 10% of scores. The input is sorted before slicing. Slices off less if proportion results in a non-integer slice index (i.e., conservatively slices off proportiontocut ).
Parameters
a array_like
Input array.
proportiontocut float
Fraction to cut off of both tails of the distribution.
axis int or None, optional
Axis along which the trimmed means are computed. Default is 0. If None, compute over the whole array a.
Returns
trim_mean ndarray
Mean of trimmed array.
* 실습
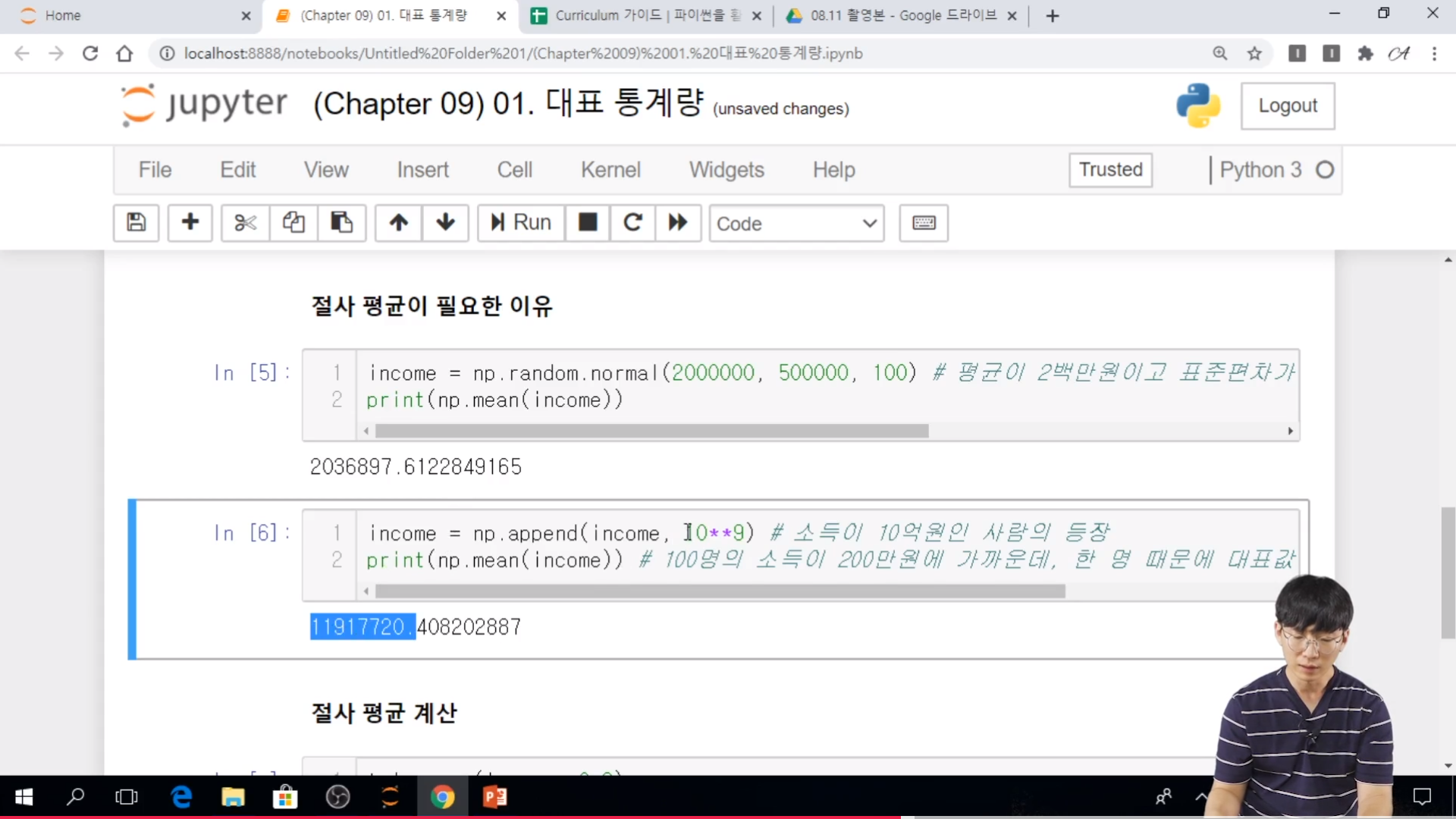
// 100명의 소득 기준으로 해야하지, 1명의 값 10억원으로 갑자기 뛰면 평균 자체가 우리가 생각하는 평균에 비해서 다르게 나온다.
// trim_mean(income, 0.2) # [20% ~ 80%] 으로 하면 원래 1명을 제외한 기대값으로 나올 수가 있다.
* 최빈값
- 한 변수가 가장 많이 취한 값을 의미하며, 범주형 변수에 대해서만 적용한다.
- 파이썬을 이용한 최빈값 계산
. scipy.stats.mode(x)
. Series.value_counts().index[0] (주의 : 최빈값이 둘 이상이면 사용 불가)
// 값의 빈도에 따라서 정의 해주는 것이다.
* 실습
[02. Part 2) 탐색적 데이터 분석 Chapter 09. 변수가 어떻게 생겼나 - 기초 통계 분석 - 03. 산포 통계량]

* 개요
- 산포란 데이터가 얼마나 퍼져있는지를 의미한다.

- 즉, 산포 통계량이란 데이터의 산포를 나타내는 통계량이라고 할 수 있다.
// 두 그래프 모두 확률 밀도 함수이다.
* 분산, 표준편차
- 편차 : 한 샘플이 평균으로부터 떨어진 거리, xi - u (xi : i 번째 관측치, u : 평균)
- 분산 : 편차의 제곱의 평균

-> 편차의 합은 항상 0이 되기 때문에, 제곱을 사용
-> 자유도가 0 (모분산)이면 n - 1 으로 나누지 않고, n 으로 나눔
- 표준편차 : 분산에 루트를 씌운 것

-> 분산에서 제곱의 영향을 없앤 지표
* 변동계수
- 분산과 표준 편차 모두 값의 스케일에 크게 영향을 받아, 상대적인 산포를 보여주는데 부적합하다.

// 상대적으로 보여 줘야 한다.
// 오른쪽을 10을 나눠줘야 한다.
- 따라서 변수를 스케일링한 뒤, 분산 혹은 표준편차를 구해야 한다.
- 만약 모든 데이터가 양수인 경우에는 변동계수(상대 표준편차)를 사용할 수 있다.
. 변동계수 = 표준편차 / 평균
* 파이썬을 이용한 분산, 표준편차, 변동계수 계산

// ddof 는 1로 잡아준다고 생각하면 된다.
// numpy.var documentation
numpy.org/doc/stable/reference/generated/numpy.var.html
numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>)Compute the variance along the specified axis.
Returns the variance of the array elements, a measure of the spread of a distribution. The variance is computed for the flattened array by default, otherwise over the specified axis.
Parameters
aarray_like
Array containing numbers whose variance is desired. If a is not an array, a conversion is attempted.
axisNone or int or tuple of ints, optional
Axis or axes along which the variance is computed. The default is to compute the variance of the flattened array.
New in version 1.7.0.
If this is a tuple of ints, a variance is performed over multiple axes, instead of a single axis or all the axes as before.
dtypedata-type, optional
Type to use in computing the variance. For arrays of integer type the default is float64; for arrays of float types it is the same as the array type.
outndarray, optional
Alternate output array in which to place the result. It must have the same shape as the expected output, but the type is cast if necessary.
ddofint, optional
“Delta Degrees of Freedom”: the divisor used in the calculation is N - ddof, where N represents the number of elements. By default ddof is zero.
keepdimsbool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.
If the default value is passed, then keepdims will not be passed through to the var method of sub-classes of ndarray, however any non-default value will be. If the sub-class’ method does not implement keepdims any exceptions will be raised.
Returns
variancendarray, see dtype parameter above
If out=None, returns a new array containing the variance; otherwise, a reference to the output array is returned.
// numpy.ndarray.var documentation
numpy.org/doc/stable/reference/generated/numpy.ndarray.var.html
method
ndarray.var(axis=None, dtype=None, out=None, ddof=0, keepdims=False)Returns the variance of the array elements, along given axis.
Refer to numpy.var for full documentation.
// pandas.Series.var documenation
pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.var.html
Series.var(axis=None, skipna=None, level=None, ddof=1, numeric_only=None, **kwargs)Return unbiased variance over requested axis.
Normalized by N-1 by default. This can be changed using the ddof argument
Parameters
axis{index (0)}skipnabool, default True
Exclude NA/null values. If an entire row/column is NA, the result will be NA.
levelint or level name, default None
If the axis is a MultiIndex (hierarchical), count along a particular level, collapsing into a scalar.
ddofint, default 1
Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements.
numeric_onlybool, default None
Include only float, int, boolean columns. If None, will attempt to use everything, then use only numeric data. Not implemented for Series.
Returns
scalar or Series (if level specified)
// numpy.std documentation
numpy.org/doc/stable/reference/generated/numpy.std.html
numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>)Compute the standard deviation along the specified axis.
Returns the standard deviation, a measure of the spread of a distribution, of the array elements. The standard deviation is computed for the flattened array by default, otherwise over the specified axis.
Parameters
aarray_like
Calculate the standard deviation of these values.
axisNone or int or tuple of ints, optional
Axis or axes along which the standard deviation is computed. The default is to compute the standard deviation of the flattened array.
New in version 1.7.0.
If this is a tuple of ints, a standard deviation is performed over multiple axes, instead of a single axis or all the axes as before.
dtypedtype, optional
Type to use in computing the standard deviation. For arrays of integer type the default is float64, for arrays of float types it is the same as the array type.
outndarray, optional
Alternative output array in which to place the result. It must have the same shape as the expected output but the type (of the calculated values) will be cast if necessary.
ddofint, optional
Means Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements. By default ddof is zero.
keepdimsbool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.
If the default value is passed, then keepdims will not be passed through to the std method of sub-classes of ndarray, however any non-default value will be. If the sub-class’ method does not implement keepdims any exceptions will be raised.
Returns
standard_deviationndarray, see dtype parameter above.
If out is None, return a new array containing the standard deviation, otherwise return a reference to the output array.
// numpy.ndarray.std documentation
numpy.org/doc/stable/reference/generated/numpy.ndarray.std.html
method
ndarray.std(axis=None, dtype=None, out=None, ddof=0, keepdims=False)Returns the standard deviation of the array elements along given axis.
Refer to numpy.std for full documentation.
// pandas.Series.std documentation
pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.std.html
Series.std(axis=None, skipna=None, level=None, ddof=1, numeric_only=None, **kwargs)Return sample standard deviation over requested axis.
Normalized by N-1 by default. This can be changed using the ddof argument
Parameters
axis{index (0)}skipnabool, default True
Exclude NA/null values. If an entire row/column is NA, the result will be NA.
levelint or level name, default None
If the axis is a MultiIndex (hierarchical), count along a particular level, collapsing into a scalar.
ddofint, default 1
Delta Degrees of Freedom. The divisor used in calculations is N - ddof, where N represents the number of elements.
numeric_onlybool, default None
Include only float, int, boolean columns. If None, will attempt to use everything, then use only numeric data. Not implemented for Series.
Returns
scalar or Series (if level specified)
// scipy.stats.variation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.variation.html
scipy.stats.variation(a, axis=0, nan_policy='propagate')Compute the coefficient of variation.
The coefficient of variation is the ratio of the biased standard deviation to the mean.
Parameters
aarray_like
Input array.
axisint or None, optional
Axis along which to calculate the coefficient of variation. Default is 0. If None, compute over the whole array a.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. The following options are available (default is ‘propagate’):
‘propagate’: returns nan
‘raise’: throws an error
‘omit’: performs the calculations ignoring nan values
Returns
variationndarray
The calculated variation along the requested axis.
* 실습
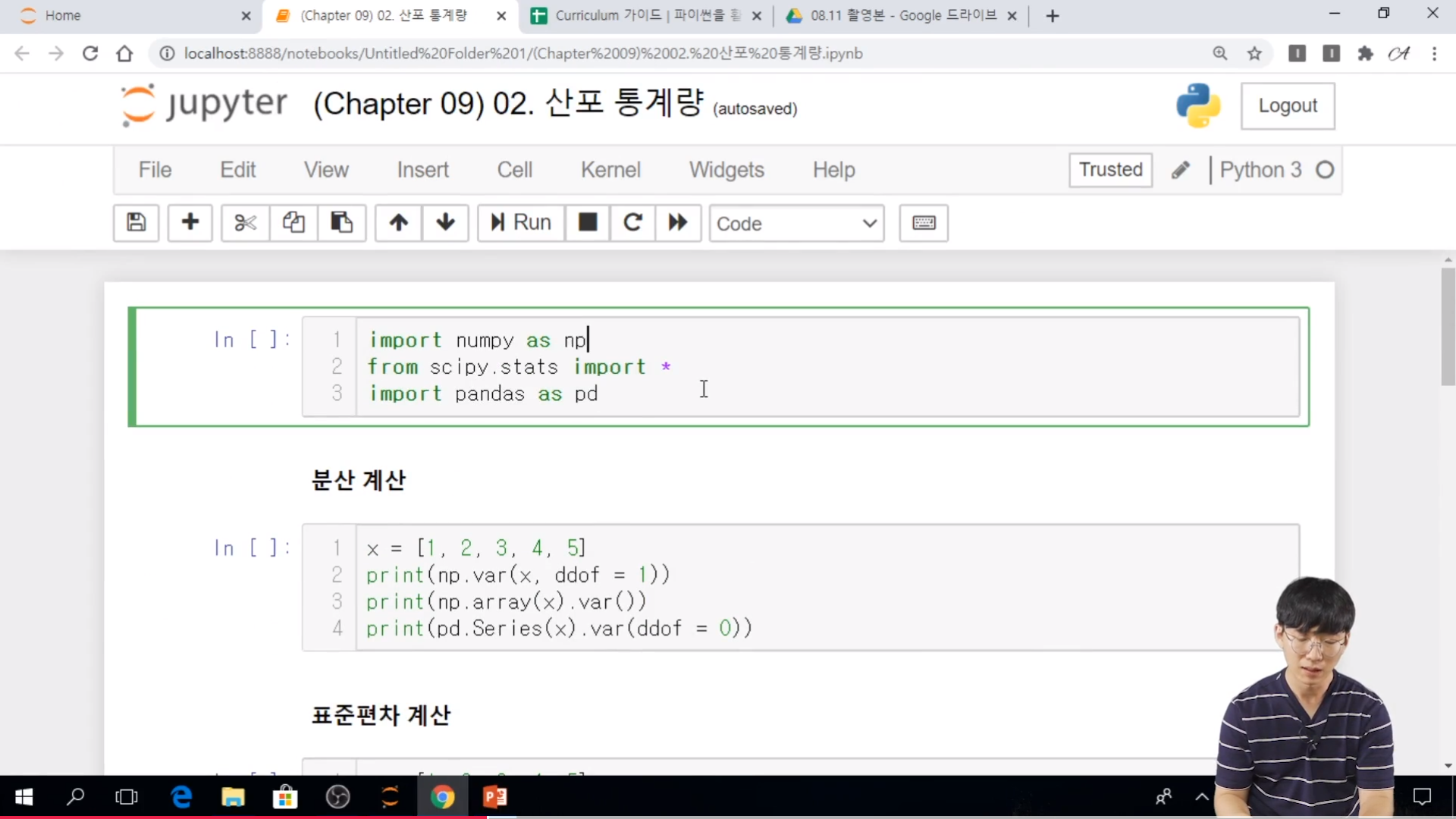
// ddof 가 가장 값이 큰데 그 이유는
- 분모 = n -1 (5 1) 로 둔 경우
// 두번째 ~ 세번째의 경우는 분모 = n 으로 둔 경우라고 생각하면 된다.
* (Tip) 둘 이상의 변수의 값을 상대적으로 비교할 때 : 스케일링
- 국어 점수가 90점인 학생과 수학 점수가 80점인 학생 중 누가 더 잘했나?
. 국어 점수 변수와 수학 점수 변수의 분포가 다르기 때문에 정확히 비교가 힘듦
. (예) 국어 점수 평균이 95점이고 수학 점수 평균이 30점이라면, 당연히 수학 점수가 80점인 학생이 더 잘한 것이다.
- 상대적으로 비교하기 위해 각 데이터에 있는 값을 상대적인 값을 갖도록 변환함

- 스케일링은 변수 간 비교 뿐만 아니라, 머신러닝에서도 널리 사용된다.
* 파이썬을 이용한 스케일링

// sklearn 머신러닝을 할때 쓰는 것이 약간 드물다고 생각하면 된다.
// sklearn.preprocessing.StandardScaler documenation
scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html
class sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)Standardize features by removing the mean and scaling to unit variance
The standard score of a sample x is calculated as:
z = (x - u) / s
where u is the mean of the training samples or zero if with_mean=False, and s is the standard deviation of the training samples or one if with_std=False.
Centering and scaling happen independently on each feature by computing the relevant statistics on the samples in the training set. Mean and standard deviation are then stored to be used on later data using transform.
Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data (e.g. Gaussian with 0 mean and unit variance).
For instance many elements used in the objective function of a learning algorithm (such as the RBF kernel of Support Vector Machines or the L1 and L2 regularizers of linear models) assume that all features are centered around 0 and have variance in the same order. If a feature has a variance that is orders of magnitude larger that others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected.
This scaler can also be applied to sparse CSR or CSC matrices by passing with_mean=False to avoid breaking the sparsity structure of the data.
Read more in the User Guide.
Parameters
copyboolean, optional, default True
If False, try to avoid a copy and do inplace scaling instead. This is not guaranteed to always work inplace; e.g. if the data is not a NumPy array or scipy.sparse CSR matrix, a copy may still be returned.
with_meanboolean, True by default
If True, center the data before scaling. This does not work (and will raise an exception) when attempted on sparse matrices, because centering them entails building a dense matrix which in common use cases is likely to be too large to fit in memory.
with_stdboolean, True by default
If True, scale the data to unit variance (or equivalently, unit standard deviation).
Attributes
scale_ndarray or None, shape (n_features,)
Per feature relative scaling of the data. This is calculated using np.sqrt(var_). Equal to None when with_std=False.
New in version 0.17: scale_
mean_ndarray or None, shape (n_features,)
The mean value for each feature in the training set. Equal to None when with_mean=False.
var_ndarray or None, shape (n_features,)
The variance for each feature in the training set. Used to compute scale_. Equal to None when with_std=False.
n_samples_seen_int or array, shape (n_features,)
The number of samples processed by the estimator for each feature. If there are not missing samples, the n_samples_seen will be an integer, otherwise it will be an array. Will be reset on new calls to fit, but increments across partial_fit calls.
// sklearn.preprocessing.MinMaxScaler
scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html
class sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1), *, copy=True)Transform features by scaling each feature to a given range.
This estimator scales and translates each feature individually such that it is in the given range on the training set, e.g. between zero and one.
The transformation is given by:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0)) X_scaled = X_std * (max - min) + min
where min, max = feature_range.
This transformation is often used as an alternative to zero mean, unit variance scaling.
Read more in the User Guide.
Parameters
feature_rangetuple (min, max), default=(0, 1)
Desired range of transformed data.
copybool, default=True
Set to False to perform inplace row normalization and avoid a copy (if the input is already a numpy array).
Attributes
min_ndarray of shape (n_features,)
Per feature adjustment for minimum. Equivalent to min - X.min(axis=0) * self.scale_
scale_ndarray of shape (n_features,)
Per feature relative scaling of the data. Equivalent to (max - min) / (X.max(axis=0) - X.min(axis=0))
New in version 0.17: scale_ attribute.
data_min_ndarray of shape (n_features,)
Per feature minimum seen in the data
New in version 0.17: data_min_
data_max_ndarray of shape (n_features,)
Per feature maximum seen in the data
New in version 0.17: data_max_
data_range_ndarray of shape (n_features,)
Per feature range (data_max_ - data_min_) seen in the data
New in version 0.17: data_range_
n_samples_seen_int
The number of samples processed by the estimator. It will be reset on new calls to fit, but increments across partial_fit calls.
Methods
|
fit(X[, y]) |
Compute the minimum and maximum to be used for later scaling. |
|
fit_transform(X[, y]) |
Fit to data, then transform it. |
|
get_params([deep]) |
Get parameters for this estimator. |
|
Undo the scaling of X according to feature_range. |
|
|
partial_fit(X[, y]) |
Online computation of min and max on X for later scaling. |
|
set_params(**params) |
Set the parameters of this estimator. |
|
transform(X) |
Scale features of X according to feature_range. |
* 실습

// Z ndarray 이므로 pd.dataframe 으로 표현
* 범위와 사분위 범위
- 범위와 사분위 범위는 산포를 나타내는 가장 직관적인 지표 중 하나임

- 사분위 범위를 IQR(iterquartile range) 라고도 하며, 이상치를 탐색할 때도 사용된다(참고: IQR Ruel)
* (참고) IQR Rule
- 변수별로 IQR 규칙을 만족하지 않는 샘플들을 판단하여 삭제하는 방법

* 파이썬을 이용한 범위 및 사분위 범위 계산

// numpy.ptp documenation
docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.ptp.html
numpy.ptp(a, axis=None, out=None, keepdims=<no value>)Range of values (maximum - minimum) along an axis.
The name of the function comes from the acronym for ‘peak to peak’.
Parameters:
| a : array_like
Input values. axis : None or int or tuple of ints, optionalAxis along which to find the peaks. By default, flatten the array. axis may be negative, in which case it counts from the last to the first axis. New in version 1.15.0. If this is a tuple of ints, a reduction is performed on multiple axes, instead of a single axis or all the axes as before. out : array_likeAlternative output array in which to place the result. It must have the same shape and buffer length as the expected output, but the type of the output values will be cast if necessary. keepdims : bool, optionalIf this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array. If the default value is passed, then keepdims will not be passed through to the ptp method of sub-classes of ndarray, however any non-default value will be. If the sub-class’ method does not implement keepdims any exceptions will be raised. |
| Returns: ptp : ndarray A new array holding the result, unless out was specified, in which case a reference to out is returned. |
// numpy.quantile documenation
numpy.org/doc/stable/reference/generated/numpy.quantile.html
numpy.quantile(a, q, axis=None, out=None, overwrite_input=False, interpolation='linear', keepdims=False)Compute the q-th quantile of the data along the specified axis.
New in version 1.15.0.
Parameters
aarray_like
Input array or object that can be converted to an array.
qarray_like of float
Quantile or sequence of quantiles to compute, which must be between 0 and 1 inclusive.
axis{int, tuple of int, None}, optional
Axis or axes along which the quantiles are computed. The default is to compute the quantile(s) along a flattened version of the array.
outndarray, optional
Alternative output array in which to place the result. It must have the same shape and buffer length as the expected output, but the type (of the output) will be cast if necessary.
overwrite_inputbool, optional
If True, then allow the input array a to be modified by intermediate calculations, to save memory. In this case, the contents of the input a after this function completes is undefined.
interpolation{‘linear’, ‘lower’, ‘higher’, ‘midpoint’, ‘nearest’}
This optional parameter specifies the interpolation method to use when the desired quantile lies between two data points i < j:
linear: i + (j - i) * fraction, where fraction is the fractional part of the index surrounded by i and j.
lower: i.
higher: j.
nearest: i or j, whichever is nearest.
midpoint: (i + j) / 2.
keepdimsbool, optional
If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original array a.
Returns
quantilescalar or ndarray
If q is a single quantile and axis=None, then the result is a scalar. If multiple quantiles are given, first axis of the result corresponds to the quantiles. The other axes are the axes that remain after the reduction of a. If the input contains integers or floats smaller than float64, the output data-type is float64. Otherwise, the output data-type is the same as that of the input. If out is specified, that array is returned instead.
// scipy.stats.iqr documenation
docs.scipy.org/doc/scipy/reference/generated/scipy.stats.iqr.html
scipy.stats.iqr(x, axis=None, rng=25, 75, scale=1.0, nan_policy='propagate', interpolation='linear', keepdims=False)Compute the interquartile range of the data along the specified axis.
The interquartile range (IQR) is the difference between the 75th and 25th percentile of the data. It is a measure of the dispersion similar to standard deviation or variance, but is much more robust against outliers [2].
The rng parameter allows this function to compute other percentile ranges than the actual IQR. For example, setting rng=(0, 100) is equivalent to numpy.ptp.
The IQR of an empty array is np.nan.
New in version 0.18.0.
Parameters
xarray_like
Input array or object that can be converted to an array.
axisint or sequence of int, optional
Axis along which the range is computed. The default is to compute the IQR for the entire array.
rngTwo-element sequence containing floats in range of [0,100] optional
Percentiles over which to compute the range. Each must be between 0 and 100, inclusive. The default is the true IQR: (25, 75). The order of the elements is not important.
scalescalar or str, optional
The numerical value of scale will be divided out of the final result. The following string values are recognized:
‘raw’ : No scaling, just return the raw IQR. Deprecated! Use scale=1 instead.
‘normal’ : Scale by 22erf−1(12)≈1.349.
The default is 1.0. The use of scale=’raw’ is deprecated. Array-like scale is also allowed, as long as it broadcasts correctly to the output such that out / scale is a valid operation. The output dimensions depend on the input array, x, the axis argument, and the keepdims flag.
nan_policy{‘propagate’, ‘raise’, ‘omit’}, optional
Defines how to handle when input contains nan. The following options are available (default is ‘propagate’):
‘propagate’: returns nan
‘raise’: throws an error
‘omit’: performs the calculations ignoring nan values
interpolation{‘linear’, ‘lower’, ‘higher’, ‘midpoint’, ‘nearest’}, optional
Specifies the interpolation method to use when the percentile boundaries lie between two data points i and j. The following options are available (default is ‘linear’):
‘linear’: i + (j - i) * fraction, where fraction is the fractional part of the index surrounded by i and j.
‘lower’: i.
‘higher’: j.
‘nearest’: i or j whichever is nearest.
‘midpoint’: (i + j) / 2.
keepdimsbool, optional
If this is set to True, the reduced axes are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the original array x.
Returns
iqrscalar or ndarray
If axis=None, a scalar is returned. If the input contains integers or floats of smaller precision than np.float64, then the output data-type is np.float64. Otherwise, the output data-type is the same as that of the input.
[파이썬을 활용한 데이터 전처리 Level UP-Comment]
- 분포를 사용하고, 스케일링에 대해서 배워 볼 수 있었다. 다소 학문적인 내용이 많아서 한번에 이해하기는 어려웠지만..
파이썬을 활용한 데이터 전처리 Level UP 올인원 패키지 Online. | 패스트캠퍼스
데이터 분석에 필요한 기초 전처리부터, 데이터의 품질 및 머신러닝 성능 향상을 위한 고급 스킬까지 완전 정복하는 데이터 전처리 트레이닝 온라인 강의입니다.
www.fastcampus.co.kr
'Programming > Python' 카테고리의 다른 글
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 13회차 미션 (0) | 2020.11.14 |
|---|---|
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 12회차 미션 (0) | 2020.11.13 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 10회차 미션 (0) | 2020.11.11 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 9 회차 미션 (0) | 2020.11.10 |
| [패스트캠퍼스 수강 후기] 데이터전처리 100% 환급 챌린지 8 회차 미션 (0) | 2020.11.09 |


